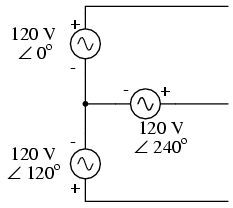
Initially we explored the idea of three-phase power systems by connecting three voltage sources together in what is commonly known as the “Y” (or “star”) configuration. This configuration of voltage sources is characterized by a common connection point joining one side of each source. (Figure below)
Three-phase “Y” connection has three voltage sources connected to a common point.
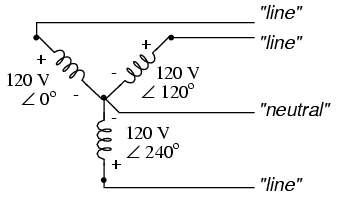
If we draw a circuit showing each voltage source to be a coil of wire (alternator or transformer winding) and do some slight rearranging, the “Y” configuration becomes more obvious in Figure.
Three-phase, four-wire “Y” connection uses a "common" fourth wire.
The three conductors leading away from the voltage sources (windings) toward a load are typically called lines, while the windings themselves are typically called phases. In a Y-connected system, there may or may not (Figure below) be a neutral wire attached at the junction point in the middle, although it certainly helps alleviate potential problems should one element of a three-phase load fail open, as discussed earlier.
Y-connected sources and loads always have line voltages greater than phase voltages, and line currents equal to phase currents. If the Y-connected source or load is balanced, the line voltage will be equal to the phase voltage times the square root of 3:
However, the “Y” configuration is not the only valid one for connecting three-phase voltage source or load elements together. Another configuration is known as the “Delta,” for its geometric resemblance to the Greek letter of the same name (Δ). Take close notice of the polarity for each winding in Figurebelow.

Three-phase, three-wire Δ connection has no common.
One quick check of this is to use Kirchhoff's Voltage Law to see if the three voltages around the loop add up to zero. If they do, then there will be no voltage available to push current around and around that loop, and consequently there will be no circulating current. Starting with the top winding and progressing counter-clockwise, our KVL expression looks something like this:
Indeed, if we add these three vector quantities together, they do add up to zero. Another way to verify the fact that these three voltage sources can be connected together in a loop without resulting in circulating currents is to open up the loop at one junction point and calculate voltage across the break: (Figure below)
Voltage across open Δ should be zero.
Starting with the right winding (120 V ∠ 120o) and progressing counter-clockwise, our KVL equation looks like this:
Sure enough, there will be zero voltage across the break, telling us that no current will circulate within the triangular loop of windings when that connection is made complete.
Having established that a Δ-connected three-phase voltage source will not burn itself to a crisp due to circulating currents, we turn to its practical use as a source of power in three-phase circuits. Because each pair of line conductors is connected directly across a single winding in a Δ circuit, the line voltage will be equal to the phase voltage. Conversely, because each line conductor attaches at a node between two windings, the line current will be the vector sum of the two joining phase currents. Not surprisingly, the resulting equations for a Δ configuration are as follows:
Let's see how this works in an example circuit: (Figure below)
The load on the Δ source is wired in a Δ.
With each load resistance receiving 120 volts from its respective phase winding at the source, the current in each phase of this circuit will be 83.33 amps:
So each line current in this three-phase power system is equal to 144.34 amps, which is substantially more than the line currents in the Y-connected system we looked at earlier. One might wonder if we've lost all the advantages of three-phase power here, given the fact that we have such greater conductor currents, necessitating thicker, more costly wire. The answer is no. Although this circuit would require three number 1 gage copper conductors (at 1000 feet of distance between source and load this equates to a little over 750 pounds of copper for the whole system), it is still less than the 1000+ pounds of copper required for a single-phase system delivering the same power (30 kW) at the same voltage (120 volts conductor-to-conductor).
One distinct advantage of a Δ-connected system is its lack of a neutral wire. With a Y-connected system, a neutral wire was needed in case one of the phase loads were to fail open (or be turned off), in order to keep the phase voltages at the load from changing. This is not necessary (or even possible!) in a Δ-connected circuit. With each load phase element directly connected across a respective source phase winding, the phase voltage will be constant regardless of open failures in the load elements.
Perhaps the greatest advantage of the Δ-connected source is its fault tolerance. It is possible for one of the windings in a Δ-connected three-phase source to fail open (Figure below) without affecting load voltage or current!
Even with a source winding failure, the line voltage is still 120 V, and load phase voltage is still 120 V. The only difference is extra current in the remaining functional source windings.
The only consequence of a source winding failing open for a Δ-connected source is increased phase current in the remaining windings. Compare this fault tolerance with a Y-connected system suffering an open source winding in Figure below.
Open “Y” source winding halves the voltage on two loads of a Δ connected load.
With a Δ-connected load, two of the resistances suffer reduced voltage while one remains at the original line voltage, 208. A Y-connected load suffers an even worse fate (Figure below) with the same winding failure in a Y-connected source
Open source winding of a "Y-Y" system halves the voltage on two loads, and looses one load entirely.
In this case, two load resistances suffer reduced voltage while the third loses supply voltage completely! For this reason, Δ-connected sources are preferred for reliability. However, if dual voltages are needed (e.g. 120/208) or preferred for lower line currents, Y-connected systems are the configuration of choice.